Новый метод определения коэффициента проницаемости пористых сред для оценки свойств грунта на примере Арктического региона

Аннотация

Коэффициент проницаемости напрямую влияет на скорость фильтрации воды в  грунте; значения скоростей фильтрации, в свою очередь, во многом определяют конструкцию и материалы [1], применяемые при возведении подземных или заглубленных в грунт сооружений.

Существует ряд методов, [2] позволяющих определить коэффициент проницаемости экспериментальными способами, однако, полученные значения имеют высокую дисперсию – результаты могут отличаться вплоть до третьего порядка, что объясняется использованием разного оборудования, техникой подготовки и текстурой исследуемых образцов, недостаточным количеством тестовых образцов, погрешностями приложенного давления, локальными неоднородностями и т.п. 

Большинство названных факторов не имеют значимости в вычислительном эксперименте, в связи с чем предлагаемый подход определения проницаемости среды основан на методе решетчатых уравнений Больцмана (LBM).

В итоге экспериментальным путем была определена зависимость проницаемости среды от коэффициента пористости на микроуровне. Впоследствии найденный закон сравнивался с результатами аналитического решения.

Представленный метод имеет высокую практическую ценность, поскольку может использоваться для определения характеристик грунта при оценке перспектив построения на нём инженерных сооружений, зданий и т.п. В частности, критическое значение имеет оценка свойств грунта в Арктике, где оттаивание грунта приводит к изменениям его поведения и влиянию на строительные объекты, размещаемые в данных районах.

Ключевые слова: местность, плотность, эксперимент, уравнение Больцмана, вычислительный эксперимент.  

Введение

Проницаемость характеризует способность пористой среды пропускать жидкость или газ и тем самым является важным параметром в строительстве [3], промышленной добыче нетрадиционной нефти [4], процессов пенообразования в пористых средах [5] и др.

Сегодня наблюдается ускорение процессов оттаивания почвы в бывших районах вечной мерзлоты в Арктической зоне. Существующие методы определения свойств грунта при планировании строительства различного рода объектов имеют низкую точность и опираются на условные коэффициенты, трудные для точного определения для конкретного грунта. В районах Арктики данная проблема усугубляется высокой динамикой изменений свойств грунта. Предложенный метод позволяет выполнить моделирование процессов в пористой среде, вычислить значение коэффициента проницаемости и построить модель его изменения.

Процесс просачивания жидкости или газа через поры пористой среды называется фильтрацией. Подходы, применяемые при моделировании процессов фильтрации жидкости в пористой среде, различаются в зависимости [1] от значений скорости течения жидкости в порах и их степени насыщенности. В случае движения жидкости в среде с ненасыщенными порами применяется уравнение Ричардса или Бринкмана; если поры находятся в насыщенном состоянии – уравнение Дарси [1-3].

В работе предполагается, что поры находятся в насыщенном состоянии, а скорости течения жидкости и число Рейнольдса малы, тогда при таких условиях для определения коэффициента проницаемости среды возможно применение линейного закона Дарси.

Точность и стабильность моделей LBM зависит от выбранного оператора столкновений. Модели [6], построенные на BGK имеют предел стабильности и низкую эффективность, кроме того BGK использует один параметр релаксации, вследствие чего возникает зависимость проницаемости от вязкости жидкости. В то же время было показано, что требуется как минимум два параметра релаксации, чтобы предупредить наличие нелинейных ошибок, зависящих от вязкости, при применении граничных условий типа упругого столкновения.

Из приведенных выше заключений можно сделать вывод, что в модели LBM следует использовать любой оператор столкновений, имеющий более одного параметра релаксации. 

LBM характеризует [7] нестационарный режим движения жидкости. Известно, что коэффициент проницаемости определяется для стационарного режима потока жидкости, который достигается в LBM после 10000-20000 итераций. Отсюда следует другая особенность LBM при определении коэффициента проницаемости – необходимость выполнения большого количества вычислений. Тем не менее, проблема высокой вычислительной сложности достаточно легко разрешается, так как одним из главных преимуществ LBM является легкость распараллеливания программного кода.

Методология

1. Метод решетчатых уравнений Больцмана

Основное уравнение LBM имеет вид [8]:

где f_i (x,t) – функция распределения, задающаяся для направления i; c_i – скорость частиц в направлении i такая, что узел x + c_i ∆t – соседний по отношению к узлу с координатами x; Ω_i – оператор столкновений; F_i – внешняя сила.

Выбор оператора столкновений обсуждался в разделе выше; в силу легкости настраивания параметров пусть в основе LBM модели будет TRT-оператор с двумя параметрами релаксации ω⁺ и ω^- [9]:

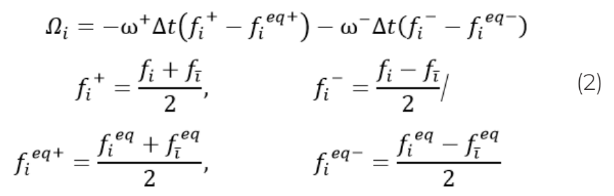
Равновесная функция распределения   [10] определяется по формуле (3):

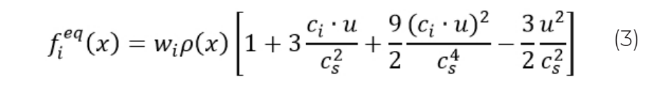
Параметры релаксации связаны соотношением [9]:

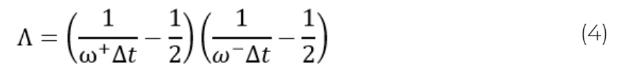
где Λ -  “магический параметр”, обуславливающий стабильность и точность TRT-оператора.

Кинематическая вязкость жидкости вычисляется по формуле:

Макроскопические параметры скорости и плотности находятся как:

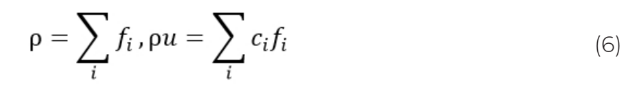
Движение жидкости происходит под действием силы тяжести. Введем ускорение g, направленное противоположно положительному направлению оси OY и имитирующее действие градиента давления, тогда [11] действующая сила: 

В верхней части рассматриваемой области жидкости, имеющей прямоугольную форму, зададим граничные условия Zou and He; в нижней – условия нулевого градиента функции распределения; слева и справа – периодические граничные условия.

В случае если границы жидкость-твердое тело находятся внутри области жидкости применяется half-way bounce-back (о котором говорится, например, в [9]), объединенный с шагом распространения частиц:

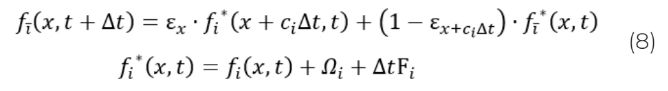
2. Закон Дарси

Коэффициент проницаемости среды (k) [12] может быть найден из уравнения Дарси:

где 〈u〉 – средняя скорость жидкости, μ – коэффициент динамической вязкости, ∇p – градиент давления; знак минуса означает, что вектор скорости направлен в сторону убывания давления.

Используем аналог коэффициента проницаемости [13] K_l, вычисляемый для дискретной решетки Больцмана и измеряющейся в l.u.², чтобы определить k.

Пусть в рассматриваемой области пористого пространства с ограничивающими поверхностями S₁,S₂ и S₃, где жидкость попадает в пористое пространство и покидает его через поверхности S₁ и  S₂,  расстояние между которыми равняется Δx_l l.u. и которые перпендикулярны направлению движения этой жидкости, действует решеточный градиент давления  между этими двумя поверхностями. Тогда Δp_l можно выразить через дифференциал плотности l:

где c_s – скорость звука.

Тогда предполагая изотропность пористой среды:

Для перехода к коэффициенту пористости, измеряемому в [м2] используем формулу (11), связывающую k и K_l:

Результаты

Достижимость установившегося течения жидкости

Изучим, как уравнение (8) определяет среднюю скорость потока жидкости и падение давления на микроуровне, в данном случае эффективный диаметр непроницаемых частиц соизмерим с Δx=1 l.u., тогда их радиус R<1 l.u.

Как уже упоминалось ранее, коэффициент проницаемости пористой среды находится только для установившихся течений жидкости, поэтому проверим достижимость стационарного режима потока. 

На рисунках 1-3 приведены графики зависимости норм Фробениуса матриц ρ_n-ρ_(n-1),u_(x,n)-u_(x,n-1),u_(y,n)-u_(y,n-1) от номера итерации n для решетки размером 25 на 25 узлов:

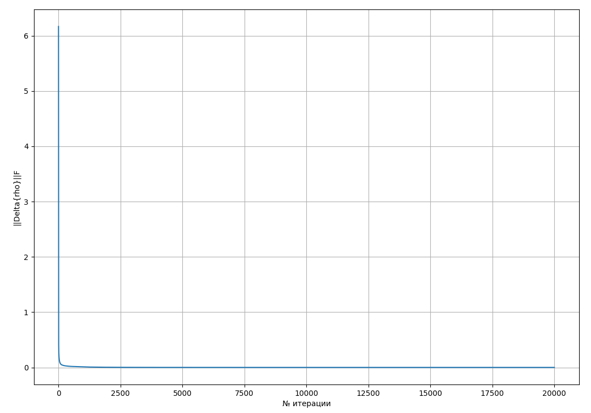
Рис. 1. График зависимости ‖n-n-1‖F от номера итерации

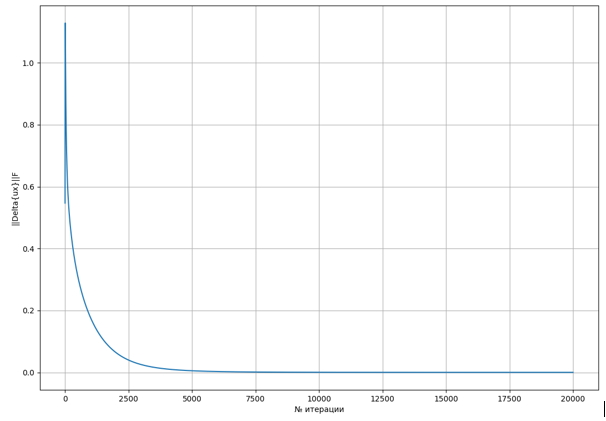
Рис. 2. График зависимости ‖ux,n-ux,n-1‖F от номера итерации

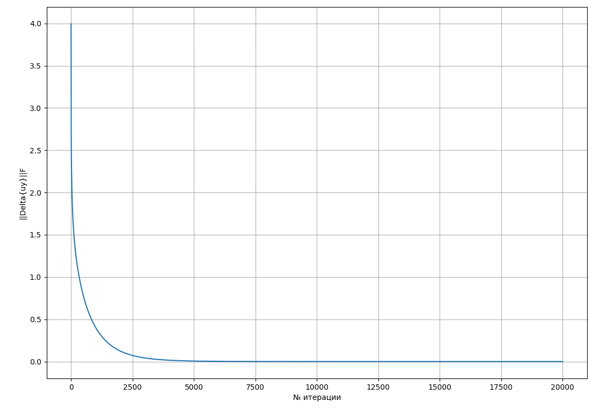
Рис. 3. График зависимости ‖uy,n-uy,n-1‖F от номера итерации

И для N = 19999 относительные значения 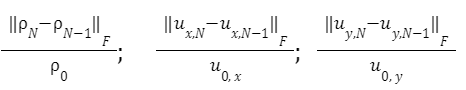, y составляют (табл. 1):

Таблица 1. Относительные значения изменений плотности и скорости жидкости

Пусть ε = 3∙10^-6,

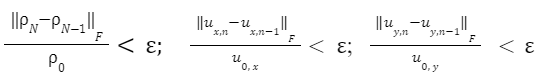(13) 

тогда соотношения (13) выполняются одновременно начиная с n = 19163. 

Таким образом, в данном случае стационарный режим течения жидкости достигается после 19163 итерации.
Аналогично посмотрим, какое число итераций необходимо для выполнения неравенств (13) для решеток размером 30 на 30 узлов, 35 на 35, 20 на 20 (табл.2).

Таблица 2. Минимальное число итераций, при котором достигается стационарный режим

Вывод эмпирического закона определения коэффициента проницаемости

Найдем зависимость коэффициента проницаемости k от пористости среды при условии, что R<1 l.u.

Валидацию закона будем проводить с помощью аналитического решения Гебарта [14]. Модель Гебарта, эквивалентная полученной, построена на предположении, что пористая структура сформирована параллельными цилиндрическими капиллярами (наглядное представление структуры рис. 4). Тогда коэффициент проницаемости определяется соотношением:

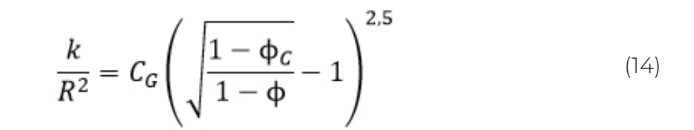
где R – радиус капилляр; Φ – коэффициент проницаемости; Φ_с – критическое значение проницаемости среды, ниже которого фильтрация жидкости не происходит; – геометрический фактор, обусловленный структурой пористой среды;  по Гебарту.

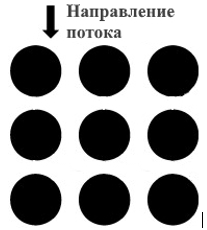
Рис. 4. Модель пористой структуры по Гебарту

Определим коэффициент проницаемости k на основе построенной модели (табл. 3); Измерение k будем выполнять в единицах Дарси,  1D =9.869233∙10^-13м².

Таблица 3. Зависимость коэффициента проницаемости от пористости




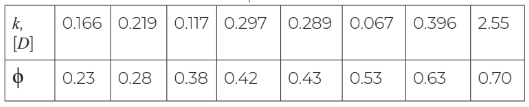
Сравним результаты таблицы 3 (рис. 5) с аналитическим решением по Гебарту (формула 14); R примем равным  0.55 l.u.:

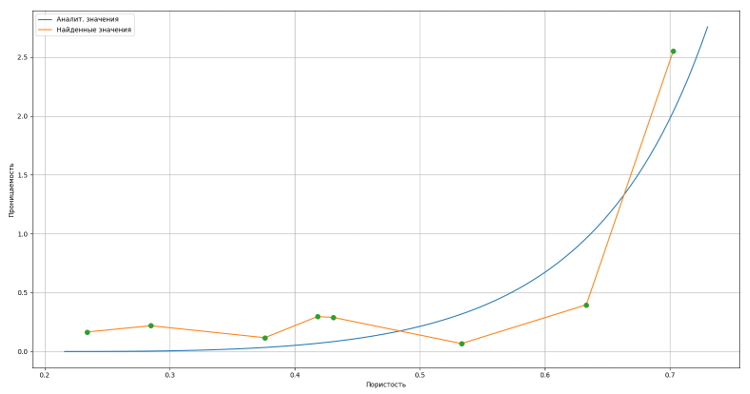
Рис. 5. Сравнение полученных результатов

Из рисунка 5 следует, что найденная с помощью модели зависимость  k _Φ  эквивалентна формуле (14) с небольшим расхождением согласно проведенному расчёту. 

Определение коэффициента проницаемости пористой среды проводилось с использованием метода решетчатых уравнений Больцмана, заданного на микроуровне. Чтобы учесть структуру порового пространства при условии соизмеримости диаметра частиц с размером 1 l.u., применялось уравнение (8), объединяющее этап потоковой передачи и граничное условие half-way bounce back.

Нахождение проницаемости возможно только для установившихся течений, вследствие чего проводилось исследование достижимости стационарного режима движения жидкости, которое показало, что минимальное необходимое число итераций составляет 20000.

Развитие Арктического региона достаточно важная и актуальная приоритетная  задача и Правительство Российской Федерации поддерживает данные программы. Освоение данного региона позволяет открывать новые возможности для РФ. Валидация модели осуществлялась с помощью выведенного Гебартом аналитического решения (14). В итоге было показано, что при радиусе частиц R = 0.55 l.u. полученная зависимость с небольшим отклонением совпадает с законом (14).

1. Polomčić, D.; Bajić, D.; Hajdin, B.; Pamučar, D. Numerical Modeling and Simulation of the Effectiveness of Groundwater Source Protection Management Plans: Riverbank Filtration Case Study in Serbia. Water 2022, 14, 1993. https://doi.org/10.3390/w14131993.
2. Zhilenkov, A. A. High productivity numerical computations for gas dynamics modelling based on DFT and approximation / A. A. Zhilenkov // Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering, ElConRus 2018, St. Petersburg and Moscow: Institute of Electrical and Electronics Engineers Inc., 2018. – P. 400-403. – DOI 10.1109/EIConRus.2018.8317117. 
3. David Grover, Surface permeability of natural and engineered porous building materials / David Grover, Cabot R. Savidge, Laura Townsend, Odanis Rosario, Liang-Bo Hu, Donna M. Rizzo, Mandar M. Dewoolkar // Construction and Building Materials, Volume 112, 2016, P. 1088-1100.
4. Eduardo Gildin, Analyzing Production Data From Hydraulically Fractured Wells: The Concept of Induced Permeability Field / Eduardo Gildin, Peter Valko, Gorgonio  Fuentes-Cruz // SPE Reservoir Evaluation & Engineering, Volume 17, 2014, 220-232.
5. Жиленков, А. А. Разработка метода решения уравнений теплопроводности с неравномерной дискретизацией для моделирования процессов в реакторах газофазной эпитаксии / А. А. Жиленков // Системы управления и информационные технологии. – 2017. – № 3(69). – С. 11-15. 
6. Farshad Gharibi, Darcy and inertial fluid flow simulations in porous media using the non-orthogonal central moments lattice Boltzmann method / Farshad Gharibi, Mahmud Ashrafizaadeh // Journal of Petroleum Science and Engineering, Volume 194, 2020.
7. Zhilenkov A.A., Chernyi S.G., Firsov A. Autonomous underwater robot fuzzy motion control system for operation under parametric uncertainties // Journal of Information Technologies and Computing Systems. 2021. № 1. С. 50-57.
8. Zhaoli Guo. Lattice Boltzmann Method and its Applications in Engineering / Zgaoli Guo, Chang Shu, et al. – World Scientific Publishing Company, 2013. – 420 p.
9. Timm Kruger. The Lattice Boltzmann Method, principles and practice / Timm Kruger, Halim Kusumaatmaja, Alexandr Kuzmin, Orest Shardt, Goncalo Silva, Erlend Magnus Viggen. – Switzerland: Springer 2017. – 694.
10. Michael C. Sukop. Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers / Michael C. Sukop, Daniel T. Thorne, Jr. - Berlin Heidelberg: Springer, 2006. – 173.
11. Sauro Succi, The Lattice Boltzmann Equation / Sauro Succi. – United Kingdom: Oxford University press 2018. – 761.
12. Radmila Mandzhieva, Practical aspects of absolute permeability finding for the lattice Boltzmann method and pore network modeling / Radmila Mandzhieva, Rimma Subhankulova // Physica A: Statistical Mechanics and its Applications, Volume 582, 2021.
13. Mohamad Chaaban, Upscaling LBM-TPM simulation approach of Darcy and non-Darcy fluid flow in deformable, heterogeneous porous media / Chaaban Mohamad, Heider Yousef, Markert Bernd // International Journal of Heat and Fluid Flow, Volume 83, 2020, 108566.
14. A. Ebrahimi Khabbazi, Developing a new form of the Kozeny–Carman parameter for structured porous media through lattice-Boltzmann modeling / A. Ebrahimi Khabbazi, J.S. Ellis, A. Bazylak // Computers & Fluids, Volume 75, 2013, Pages 35-41.

1. Polomčić, D.; Bajić, D.; Hajdin, B.; Pamučar, D. Numerical Modeling and Simulation of the Effectiveness of Groundwater Source Protection Management Plans: Riverbank Filtration Case Study in Serbia. Water 2022, 14, 1993. https://doi.org/10.3390/w14131993.
2. Zhilenkov, A. A. High productivity numerical computations for gas dynamics modelling based on DFT and approximation / A. A. Zhilenkov // Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering, ElConRus 2018, St. Petersburg and Moscow: Institute of Electrical and Electronics Engineers Inc., 2018. – P. 400-403. – DOI 10.1109/EIConRus.2018.8317117. – EDN YBVRYL.
3. David Grover, Surface permeability of natural and engineered porous building materials / David Grover, Cabot R. Savidge, Laura Townsend, Odanis Rosario, Liang-Bo Hu, Donna M. Rizzo, Mandar M. Dewoolkar // Construction and Building Materials, Volume 112, 2016, Pages 1088-1100.
4. Eduardo Gildin, Analyzing Production Data From Hydraulically Fractured Wells: The Concept of Induced Permeability Field / Eduardo Gildin, Peter Valko, Gorgonio  Fuentes-Cruz // SPE Reservoir Evaluation & Engineering, Volume 17, 2014, 220-232.
5. ZHilenkov, A. A. Razrabotka metoda resheniya uravnenij teploprovodnosti s neravnomernoj diskretizaciej dlya modelirovaniya processov v reaktorah gazofaznoj epitaksii / A. A. ZHilenkov // Sistemy upravleniya i informacionnye tekhnologii. – 2017. – № 3(69). – S. 11-15. – EDN ZDGMVR.
6. Farshad Gharibi, Darcy and inertial fluid flow simulations in porous media using the non-orthogonal central moments lattice Boltzmann method / Farshad Gharibi, Mahmud Ashrafizaadeh // Journal of Petroleum Science and Engineering, Volume 194, 2020.
7. Zhilenkov A.A., Chernyi S.G., Firsov A. Autonomous underwater robot fuzzy motion control system for operation under parametric uncertainties // Journal of Information Technologies and Computing Systems. 2021. № 1. S. 50-57.
8. Zhaoli Guo. Lattice Boltzmann Method and its Applications in Engineering / Zgaoli Guo, Chang Shu, et al. – World Scientific Publishing Company, 2013. – 420 p.
9. Timm Kruger. The Lattice Boltzmann Method, principles and practice / Timm Kruger, Halim Kusumaatmaja, Alexandr Kuzmin, Orest Shardt, Goncalo Silva, Erlend Magnus Viggen. – Switzerland: Springer 2017. – 694.
10. Michael C. Sukop. Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers / Michael C. Sukop, Daniel T. Thorne, Jr. - Berlin Heidelberg: Springer, 2006. – 173.
11. Sauro Succi, The Lattice Boltzmann Equation / Sauro Succi. – United Kingdom: Oxford University press 2018. – 761.
12. Radmila Mandzhieva, Practical aspects of absolute permeability finding for the lattice Boltzmann method and pore network modeling / Radmila Mandzhieva, Rimma Subhankulova // Physica A: Statistical Mechanics and its Applications, Volume 582, 2021.
13. Mohamad Chaaban, Upscaling LBM-TPM simulation approach of Darcy and non-Darcy fluid flow in deformable, heterogeneous porous media / Chaaban Mohamad, Heider Yousef, Markert Bernd // International Journal of Heat and Fluid Flow, Volume 83, 2020, 108566.
14. A. Ebrahimi Khabbazi, Developing a new form of the Kozeny–Carman parameter for structured porous media through lattice-Boltzmann modeling / A. Ebrahimi Khabbazi, J.S. Ellis, A. Bazylak // Computers & Fluids, Volume 75, 2013, Pages 35-41.